More content：力扣题记之动态规划

70. 爬楼梯✅

dp数组下标代表当前在第几阶，数组value表示到这一阶的方法数（即爬到第i层楼梯，有dp[i]种方法）

遍历顺序从前往后 但是一开始没想明白为什么状态转移公式是dp[i] = dp[i-1] + dp[i-2] 只是找规律推出来的

class Solution {
public:
    int climbStairs(int n) {
        vector<int> dp(50); //dp数组下标代表当前在第几阶，数组value表示到这一阶的方法数
        dp[1] = 1;
        dp[2] = 2;
        if(n < 3) return dp[n];
        for(int i = 3; i <= n; i++) dp[i] = dp[i-1] + dp[i-2];

        return dp[n];
    }
};

---

118. 杨辉三角✅

dp数组含义：dp[i][j]为第i+1行的第j+1个数值

依据杨辉三角的定义模拟DP即可

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> dp;
        for(int i = 0; i < numRows; i++) {
            vector<int> v(i+1, 0);
            dp.push_back(v);
            dp[i][0] = 1;
            dp[i][i] = 1;
        }
 
        for(int i = 2; i < numRows; i++) {
            for(int j = 1; j < i; j++) {
                dp[i][j] = dp[i-1][j-1] + dp[i-1][j];
            }
        }
        
        return dp;
    }
};

---

198. 打家劫舍✅

dp数组含义：前i间房屋能偷的最高金额为dp[i]

初始化：dp[0]=nums[0]（下标为0也就是第一间房屋，能偷的最高金额自然为nums[0]），dp[1] = max(nums[0], nums[1])（相邻的两间房只能偷一个，因此哪个金额高就偷哪个）

class Solution {
public:
    int rob(vector<int>& nums) {
        if(nums.size() == 1) return nums[0];

        vector<uint64_t> dp(nums.size() + 1, 0);
        dp[0] = nums[0];
        dp[1] = max(nums[0], nums[1]);

        for(int i = 2; i < nums.size(); i++) {
            dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]); //第i家偷or不偷
            // cout << "dp[" << i << "] = " << dp[i] << endl;
        }

        return dp[nums.size()-1];   
    }
};

---

279. 完全平方数❌

没想到是完全背包问题!

每个完全平方数都可以重复用 因此完全背包

求最少数量 跟322. 零钱兑换很相似 只需要把物品从硬币换成完全平方数即可

class Solution {
public:
    int numSquares(int n) {
        //当n为i时，凑满n需要的最少完全平方数的个数为dp[i]
        vector<int> dp(n + 1, INT_MAX);
        dp[0] = 0;

        for(int i = 1; i * i < 10001; i++) {
            for(int j = i * i; j <= n; j++) {
                dp[j] = min(dp[j], dp[j-i*i] + 1);
            }
        }

        return dp[n];
    }
};

---

322. 零钱兑换✅

跟上题279. 完全平方数同理 完全背包

注意数组数据类型为uint64_t 否则会溢出

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        //凑成总金额i的最少硬币个数为dp[i]
        vector<uint64_t> dp(amount + 1, INT_MAX);
        dp[0] = 0;

        for(int i = 0; i < coins.size(); i++) {
            for(int j = coins[i]; j <= amount; j++) {
                dp[j] = min(dp[j], dp[j-coins[i]] + 1);
            }
        }

        if(dp[amount] == INT_MAX) return -1;
        return dp[amount];
    }
};

---

139. 单词拆分❌

完全背包 但这是一个排列问题 因此在遍历时必须先遍历容量再遍历物品

否则对于示例2：s = “applepenapple”, wordDict = [“apple”, “pen”] apple只会出现在头部 而不会再次出现在尾部 因为物品遍历一次就没了 其它容量来继承它的状态 apple也只会出现在头部

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        //拼出目标字符串前i个字符所需要的最少单词数为dp[i]
        vector<uint64_t> dp(s.size()+1, INT_MAX);
        dp[0] = 0;

        for(int i = 0; i <= s.size(); i++) {//先遍历容量
            for(int j = 0; j < wordDict.size(); j++) { //再遍历物品
                if(i >= wordDict[j].size() && s.substr(i-wordDict[j].size(), wordDict[j].size()) == wordDict[j]) {
                    dp[i] = min(dp[i], dp[i-wordDict[j].size()] + 1); 
                } 
            }
        }

        if(dp[s.size()] == INT_MAX) return false;
        return true;
    }
};

---

※300. 最长递增子序列✅两个变式

dp数组含义：下标从0到i的最长递增子序列的长度是dp[i]

先遍历长度，再遍历之前的每一个状态

扩展1：现在不要求输出长度，而是最长递增子序列本身（如果有多个，输出任意一个）

扩展2：现在不要求输出长度，而是最长递增子序列本身（如果有多个，输出字典序最小的那个）

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        //下标从0到i的最长递增子序列的长度是dp[i]
        vector<int> dp(nums.size() + 1, 1);
        int res = 1;

        for(int i = 1; i < nums.size(); i++) {
            for(int j = 0; j < i; j++) {
                if(nums[j] < nums[i]) dp[i] = max(dp[i], dp[j] + 1);
            }  
            res = max(res, dp[i]);
            // cout << "dp[" << i << "] = " << dp[i] << endl;
        }

        return res;
    }
};

class 扩展1 {
public:
    int lengthOfLIS(vector<int>& nums) {
        int max_len = 1; // 最长递增子序列的长度
        int end_index = 0; // 最长递增子序列的尾部索引
        // 数组下标[0:i]的最长递增子序列的长度为dp[i]
        vector<int> dp(nums.size(), 1);
        // 记录每个位置的前驱节点
        vector<int> prev(nums.size(), -1);
        for(int i = 1; i < nums.size(); i++) {
            for(int j = 0; j < i; j++) {
                if(nums[i] > nums[j] && dp[j] + 1 > dp[i]) {
                    dp[i] = dp[j] + 1;
                    prev[i] = j; // 更新前驱节点
                }  
            }
            if(dp[i] > max_len) {
                max_len = dp[i];
                end_index = i;
            }
        }
        // 回溯构造最长递增子序列
        vector<int> lis;
        while(end_index != -1) {
            lis.push_back(nums[end_index]);
            end_index = prev[end_index];
        }
        reverse(lis.begin(), lis.end());
        
        for(int &x : lis) cout << x << " ";
        
        return 1;
    }
};

class 扩展2 {
public:
    int lengthOfLIS(vector<int>& nums) {
        int max_len = 1; // 最长递增子序列的长度
        int end_index = 0; // 最长递增子序列的尾部索引
        // 数组下标[0:i]的最长递增子序列的长度为dp[i]
        vector<int> dp(nums.size(), 1);
        // 记录每个位置的前驱节点
        vector<int> prev(nums.size(), -1);
        for(int i = 1; i < nums.size(); i++) {
            for(int j = 0; j < i; j++) {
                if(nums[i] > nums[j]) {
                    if(dp[j] + 1 > dp[i]) { // 能延长子序列
                        dp[i] = dp[j] + 1;
                        prev[i] = j; // 更新前驱节点
                    } else if(dp[j] + 1 == dp[i]) { // 长度相同，选择字典序更小的
                        if(prev[i] == -1 || nums[j] < nums[prev[i]]) {
                            prev[i] = j; 
                        }
                    }
                    
                }  
            }
            // 更新最长子序列的尾部索引
            if(dp[i] > max_len) {
                max_len = dp[i];
                end_index = i;
            } else if(dp[i] == max_len) {
                // 如果长度相同，选择字典序的那个
                if(nums[i] < nums[end_index]) end_index = i;
            }
        }
        // 回溯构造最长递增子序列
        vector<int> lis;
        while(end_index != -1) {
            lis.push_back(nums[end_index]);
            end_index = prev[end_index];
        }
        reverse(lis.begin(), lis.end());
        
        for(int &x : lis) cout << x << " ";
        
        return 1;
    }
};

---

152. 乘积最大子数组❌

连续的子序列问题 本题是 53. 最大子数组和 的乘法版本

没想到要用两个dp数组

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int res = -INT_MAX;
        if(nums.size() == 1) return nums[0];
        //以下标i结尾的连续子数组的最大乘积为dpMax[i]
        //以下标i结尾的连续子数组的最小乘积为dpMin[i]
        vector<int> dpMax(nums.size() + 1, 0);
        vector<int> dpMin(nums.size() + 1, 0);
        dpMax[0] = nums[0];
        dpMin[0] = nums[0];
 
        for(int i = 1; i < nums.size(); i++) {
            //{} 是初始化列表的语法，用于让 std::max 同时处理多个值 
            dpMax[i] = max({nums[i] * dpMax[i-1], nums[i] * dpMin[i-1], nums[i]});
            dpMin[i] = min({nums[i] * dpMax[i-1], nums[i] * dpMin[i-1], nums[i]});
        }

        return ranges::max(dpMax);
    }
};

---

416. 分割等和子集✅

一眼01背包变式 物品的重量和价值相等

背包容量设为元素总和一半 看能否恰好塞入若干元素即可

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        //01背包
        int sum = 0;
        for(const auto &i : nums) sum += i;

        if(sum % 2) return false; //奇数

        sum /= 2; //背包容量
        vector<int> dp(sum + 1, 0);

        for(int i = 0; i < nums.size(); i++) {
            for(int j = sum; j >= nums[i]; j--) {
                dp[j] = max(dp[j], dp[j-nums[i]]+nums[i]);
                // cout << "i = " << i << ", dp[" << j << "] = " << dp[j] << endl;
            }
        }

        if(dp[sum] == sum) return true; //恰好装进去
        return false; 
    }
};

---

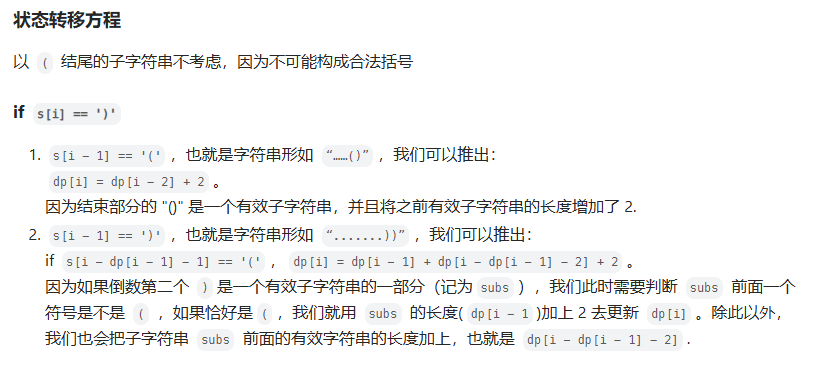
32. 最长有效括号❌

连续的子序列问题

状态转移方程没想出来

class Solution {
public:
    int longestValidParentheses(string s) {
        if(s.size() < 2) return 0;
        //以下标i结尾的最长有效括号子串长度是dp[i]
        vector<int> dp(s.size(), 0);
  

        for(int i = 1; i < s.size(); i++) {
            if(s[i] == '(') continue; //只考虑')'
            
            if(s[i-1] == '(') {
                if(i >= 2) dp[i] = dp[i-2] + 2;
                else dp[i] = 2; //考虑情况：i = 1, s = "()"
            } else if(i - dp[i-1] - 1 >= 0 && s[i - dp[i-1] - 1] == '(') { //考虑情况：i = 9, s = "()(()()())"
                if(i- dp[i-1] - 2 >= 0) dp[i] = dp[i-1] + dp[i- dp[i-1] - 2] + 2; //把中断的也连上，如果有的话，比如上面样例的前两个字符"()"
                else dp[i] = dp[i-1] + 2;
            }
            // cout << "dp[" << i << "] = " << dp[i] << endl;
        }

        return ranges::max(dp);
    }
};

---

62. 不同路径✅

只能往左或往下走 那么一个状态就可以从左边格子和上边格子的状态继承而来

dp数组含义：到达下标为(i,j)位置的路径有dp[i][j]条 第一行和第一列的路径都只有一条

class Solution {
public:
    int uniquePaths(int m, int n) {
        //到达下标为(i,j)位置的路径有dp[i][j]条
        vector<vector<int>> dp(m, vector<int>(n, 0));

        for(int i = 0; i < m; i++) dp[i][0] = 1;
        for(int i = 0; i < n; i++) dp[0][i] = 1;

        for(int i = 1; i < m; i++) {
            for(int j = 1; j < n; j++) {
                dp[i][j] = dp[i-1][j] + dp[i][j-1]; 
            }
        }

        return dp[m-1][n-1];
    }
};

---

64. 最小路径和✅

思路和62. 不同路径基本一致

dp数组含义：到达下标为(i,j)位置的路径有dp[i][j]条 第一行和第一列的路径都只有一条

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int row = grid.size();
        int col = grid[0].size();
        //到达下标为(i,j)位置的最小路径数字总和为dp[i][j]
        vector<vector<int>> dp(row, vector<int>(col, 0));
        dp[0][0] = grid[0][0];
        for(int i = 1; i < row; i++) dp[i][0] = grid[i][0] + dp[i-1][0];
        for(int j = 1; j < col; j++) dp[0][j] = grid[0][j] + dp[0][j-1];

        for(int i = 1; i < row; i++) {
            for(int j = 1; j < col; j++) {
                dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]; 
            }
        }

        return dp[row-1][col-1];
    }
};

---

5. 最长回文子串❌

忘记回文的子串怎么处理了

DP数组含义：表示区间范围[i,j]的子串是否是回文子串，如果是，则dp[i][j]为true，否则为false

遍历顺序见：代码随想录647. 回文子串

class Solution {
public:
    string longestPalindrome(string s) {
        //表示区间范围[i,j]的子串是否是回文子串，如果是，则dp[i][j]为true，否则为false
        vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
        string res = s.substr(0, 1); //回文串默认取s的第一个字符
        int max_len = 1;
        for(int i = s.size(); i >= 0; i--) {
            for(int j = i; j < s.size(); j++) { //根据dp数组的定义，j >= i
                if(s[i] == s[j]) {
                    if(j - i <= 1) {
                        dp[i][j] = true;
                        if(j - i + 1 > max_len) {
                            max_len = j - i + 1;
                            res = s.substr(i, j - i + 1);
                        }
                    } else if(dp[i+1][j-1]) { // 两种情况可以合并在一起，这里只是为了分清是不同的情况
                        dp[i][j] = true;
                        if(j - i + 1 > max_len) {
                            max_len = j - i + 1;
                            res = s.substr(i, j - i + 1);
                        }
                    }
                }
            }
        }

        return res;
    }
};

---

1143. 最长公共子序列❌

无思路

dp数组含义：text1的[0, i-1]部分与text2的[0, j-1]部分的最长公共子序列为dp[i][j]

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        // text1的[0, i-1]部分与text2的[0, j-1]部分的最长公共子序列为dp[i][j]
        vector<vector<int>> dp(text1.size()+1, vector<int>(text2.size()+1, 0));
        int res = 0;
        for(int i = 1; i <= text1.size(); i++) {
            for(int j = 1; j <= text2.size(); j++) {
                if(text1[i-1] == text2[j-1]) {
                    dp[i][j] = dp[i-1][j-1] + 1;
                } else {
                    dp[i][j] = max(dp[i][j-1], dp[i-1][j]);
                }
                // cout << "dp[" << i << "][" << j << "] = " << dp[i][j] << endl;
                res = max(res, dp[i][j]);
            }
        }
 
        return res;
    }
};

---

72. 编辑距离❌

没什么思路

dp数组含义：以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]（即word1中前i个字母组成的字符串，和word2中前j个字母组成的字符串，最近编辑距离为dp[i][j]）

共四种情况：无需编辑、删除word1的一个字母、删除word2的一个字母、替换一个字母

class Solution {
public:
    int minDistance(string word1, string word2) {
        //以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]
        vector<vector<int>> dp(word1.size()+1, vector<int>(word2.size()+1, 0));

        for(int i = 0; i <= word1.size(); i++) dp[i][0] = i;
        for(int i = 0; i <= word2.size(); i++) dp[0][i] = i;

        for(int i = 1; i <= word1.size(); i++) {
            for(int j = 1; j <= word2.size(); j++) {
                if(word1[i-1] == word2[j-1]) dp[i][j] = dp[i-1][j-1];
                else dp[i][j] = min({dp[i-1][j-1], dp[i-1][j], dp[i][j-1]}) + 1;    
            }
        }

        return dp[word1.size()][word2.size()];
    }
};